陆拾壹的博客

一只超会写bug的程序猿

0%

力扣每日一题2021/9/27

发表于 更新于 分类于 ， 阅读次数：

题目：85. 最大矩形

给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

难度：困难

示例 1：

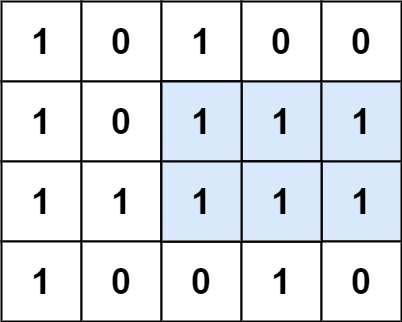
输入：matrix = [[“1”,”0”,”1”,”0”,”0”],[“1”,”0”,”1”,”1”,”1”],[“1”,”1”,”1”,”1”,”1”],[“1”,”0”,”0”,”1”,”0”]]
输出：6
解释：最大矩形如上图所示。

示例 2：

输入：matrix = []
输出：0

示例 3：

输入：matrix = [[“0”]]
输出：0

示例 4：

输入：matrix = [[“1”]]
输出：1

示例 5：

输入：matrix = [[“0”,”0”]]
输出：0

提示：

  • rows == matrix.length
  • cols == matrix[0].length
  • 0 <= rows, cols <= 200
  • matrix[i][j] 为 '0' 或 '1'

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximal-rectangle
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解题思路

  1. 使用柱状图的优化暴力方法
  2. 单调栈

解题代码

使用柱状图的优化暴力方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
    public int maximalRectangle(char[][] matrix) {
        if (matrix == null || matrix.length == 0) {
            return 0;
        }
        int m = matrix.length, n = matrix[0].length;
        int[][] left = new int[m][n];
        int ans = 0;
        for (int i = 0; i < m; i++) {
            left[i][0] = Integer.valueOf(matrix[i][0] - '0');
        }

        for (int i = 0; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (matrix[i][j] == '1') {
                    left[i][j] = left[i][j - 1] + 1;
                } else {
                    left[i][j] = 0;
                }
            }
        }

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (matrix[i][j] == '1') {
                    int k = i;
                    int minLen = left[i][j];
                    while (k >= 0) {
                        if (minLen > left[k][j]) {
                            minLen = left[k][j];
                        }
                        k--;
                        ans = Math.max(ans, (i - k) * minLen);
                    }
                }
            }
        }
        return ans;
    }
}

官方解题代码

单调栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
    public int maximalRectangle(char[][] matrix) {
        int m = matrix.length;
        if (m == 0) {
            return 0;
        }
        int n = matrix[0].length;
        int[][] left = new int[m][n];

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (matrix[i][j] == '1') {
                    left[i][j] = (j == 0 ? 0 : left[i][j - 1]) + 1;
                }
            }
        }

        int ret = 0;
        for (int j = 0; j < n; j++) { // 对于每一列，使用基于柱状图的方法
            int[] up = new int[m];
            int[] down = new int[m];

            Deque<Integer> stack = new LinkedList<Integer>();
            for (int i = 0; i < m; i++) {
                while (!stack.isEmpty() && left[stack.peek()][j] >= left[i][j]) {
                    stack.pop();
                }
                up[i] = stack.isEmpty() ? -1 : stack.peek();
                stack.push(i);
            }
            stack.clear();
            for (int i = m - 1; i >= 0; i--) {
                while (!stack.isEmpty() && left[stack.peek()][j] >= left[i][j]) {
                    stack.pop();
                }
                down[i] = stack.isEmpty() ? m : stack.peek();
                stack.push(i);
            }

            for (int i = 0; i < m; i++) {
                int height = down[i] - up[i] - 1;
                int area = height * left[i][j];
                ret = Math.max(ret, area);
            }
        }
        return ret;
    }
}