序言

以前在数据结构与算法中看过根据后缀表达式（逆波兰表达式）求值的内容，当时时间少对其也不是很在意就水了过去，现在重新学起时感觉该算法思想十分玄妙好用，学习完自己写了波代码，顺便整理总结下以便日后遗忘时能够快速复习或者有新的理解时回来看看。

简介

逆波兰表达式，又叫做后缀表达式。逆波兰表示法是波兰逻辑学家J·卢卡西维兹(J·Lukasiewicz)于1929年首先提出的一种表达式的表示方法。后来,人们就把用这种表示法写出的表达式称作“逆波兰表达式”。逆波兰表达式把运算量写在前面,把运算符写在后面。相对于后缀表达式，还有前缀表达式（波兰表达式）、中缀表达式。

举例

前缀表达式：- + 1 * + 2 3 5 / 6 2
中缀表达式：1 + ( ( 2 + 3 ) * 5 ) - 6 / 2
后缀表达式：1 2 3 + 5 * + 6 2 / -

逆波兰表达式的意义

上述例子中，不难看出中缀表达式就是我们平时计算的式子，另外两个看得满脑子问号，我初学时也是如此，甚至一度觉得有中缀表达式就够了，为啥还要多整些花里胡哨的，这不是闲着吗？所以我一开始也没有多在意就水过去了，直到重新学习时才发现，真香！真牛批！！！中缀表达式是我们平时生活中计算使用的表达式，我们经过后天学习已经习惯并善于计算这样的表达式。对于人类来说，中缀表达式简单易懂，后缀表达式复杂难懂，而对于计算机来说，却是相反的，中缀表达式对计算机而言是十分复杂的结构，而后缀表达式反而简单易懂，这是因为计算机普遍采用的内存结构是栈式结构，也就是执行先进后出的顺序。

计算逆波兰表达式

需求

现有一个逆波兰表达式1 2 3 + 5 * + 6 2 / -，要求写一个逆波兰计算器计算结果

思路

创建一个数栈numStack
若字符为数字，直接压入数栈
若字符为运算符，则数栈弹出两个数进行计算，并将结果压入数栈
最后数栈只会剩下一个元素，返回栈顶元素，即为结果

步骤分析

1.字符1、2、3皆为数字压入数栈

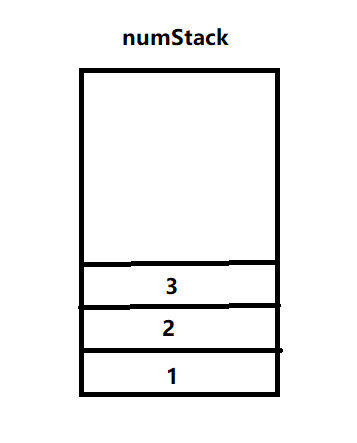
2.匹配到字符+，弹出两个数3和2进行计算，并将结果压入数栈

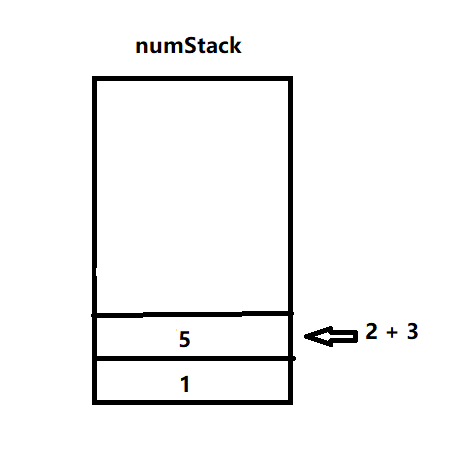
3.字符5入栈

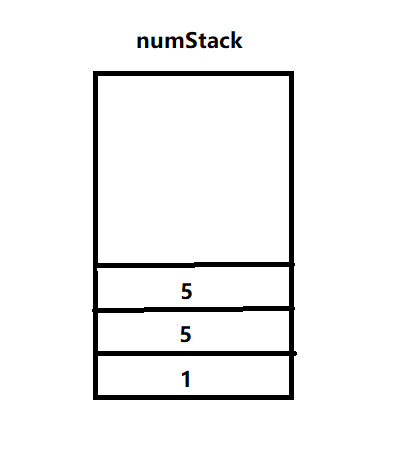
4.匹配到字符*，弹出两个数5和5进行计算，并将结果压入数栈

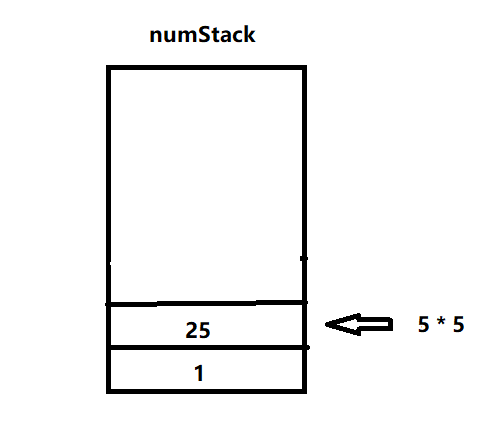
5.匹配到字符+，弹出两个数25和1进行计算，并将结果压入数栈

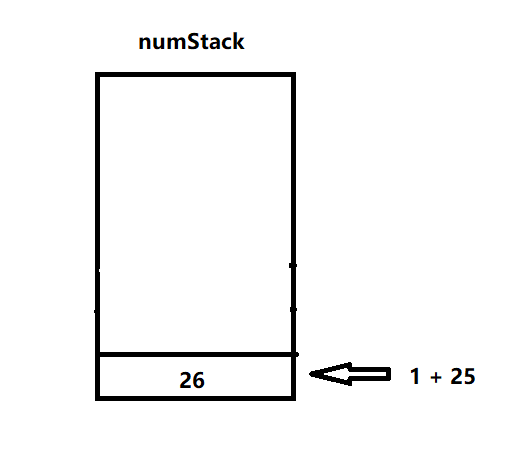
6.字符6、2压入数栈

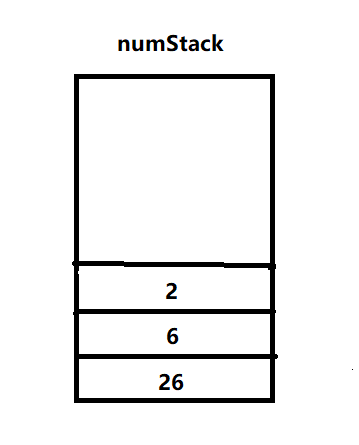
7.匹配到字符/，弹出两个数2和6进行计算，并将结果压入数栈

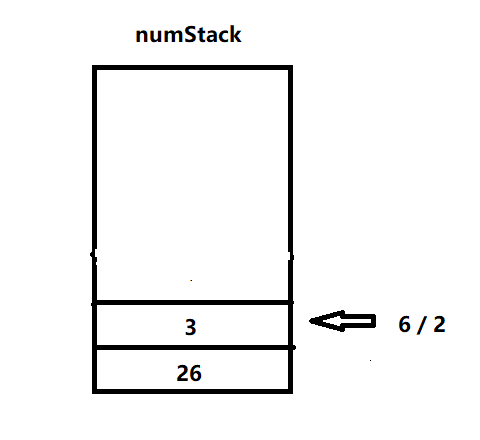
8.匹配到字符-，弹出两个数3和26进行计算，并将结果压入数栈，循环结束，栈中元素即为结果

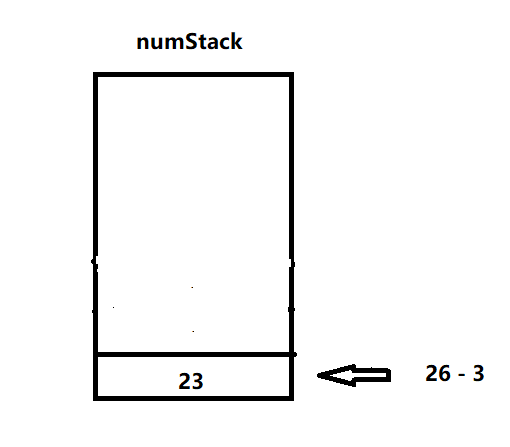
实现代码

import java.util.Stack;

public class PolandCalculator {
    public String suffix;
    public PolandCalculator(String suffix) {
        this.suffix = suffix;
    }

    public int calculate() {
        Stack<String> numStack = new Stack<>();
        String[] str = suffix.split(" ");
        int res = 0;
        for (String s : str) {
            if (!isOperator(s)) {
                numStack.push(s);
            }else {
                res = compute(s, Integer.parseInt(numStack.pop()), Integer.parseInt(numStack.pop()));
                numStack.push(String.valueOf(res));
            }
        }
        return Integer.parseInt(numStack.pop());
    }

    public boolean isOperator(String oper) {
        return oper.equals("+") || oper.equals("-") || oper.equals("*") || oper.equals("/");
    }

    public int compute(String oper, int num1, int num2) {
        switch (oper) {
            case "+" : num2 += num1; break;
            case "-" : num2 -= num1; break;
            case "*" : num2 *= num1; break;
            case "/" : num2 /= num1; break;
        }
        return num2;
    }
}

问题

逆波兰计算器可以并且只能计算逆波兰表达式，但对于我们来说，逆波兰表达式相对复杂，我们更习惯于书写中缀表达式，所以我们能不能输入中缀表达式，而让计算机计算后缀表达式呢？当然可以，我们将中缀表达式转换成逆波兰表达式让计算机执行，那么如何实现中缀转逆波兰呢，往下接着分析。

中缀表达式转逆波兰表达式

需求

现有一个中缀表达式1 + ( ( 2 + 3 ) * 5 ) - 6 / 2，要求将其转换成逆波兰表达式

思路

创建一个数栈numStack和一个符号栈operStack
若字符为数字，则直接入数栈
若字符为运算符：
- 若符号栈为空或栈顶元素为(，则直接入符号栈
- 若字符的优先级大于符号栈栈顶元素，则压入符号栈
- 否则，将符号栈栈顶元素出栈，压入数栈中，再将字符压入符号栈
若字符为括号：
- 若字符为左括号(，则直接入符号栈
- 若为右括号)，则将符号栈元素出栈并压入数栈直至(为止（左括号出符号栈但不入数栈）
将符号栈中剩余元素压入数栈中，并将数栈元素出栈拼接成字符串，将字符串进行一次逆序，即为所求逆波兰表达式（注意：栈的执行顺序是先进后出，此时拼接出的字符串是逆波兰表达式的反序字符串，所以最后需要进行一次逆序）

步骤分析

1.字符1入数栈，字符+满足3.1入符号栈，字符(、(满足4.1入符号栈，2入数栈，+满足3.1入符号栈，3入数栈

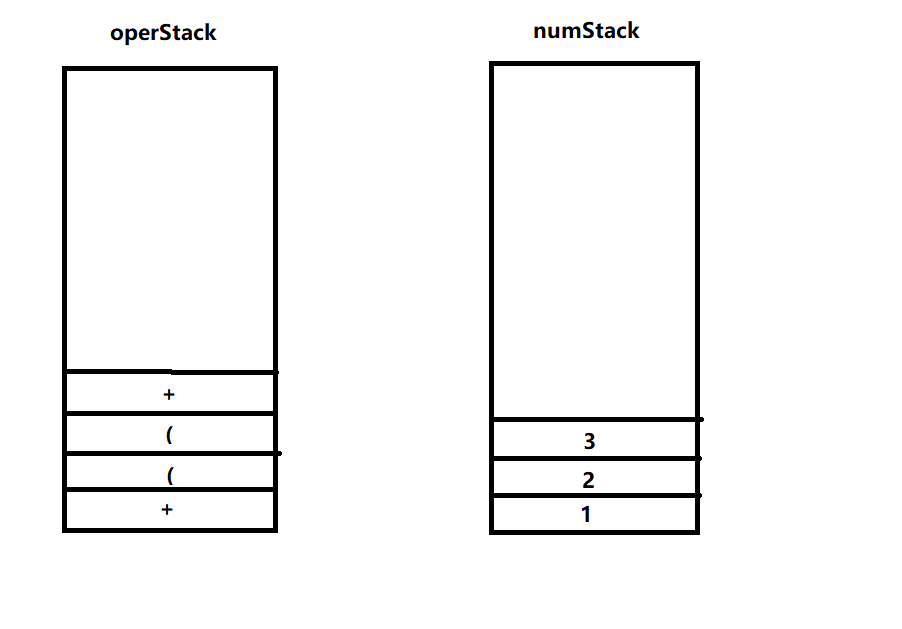
2.字符)，满足4.2，将符号栈元素出栈并压入数栈直至(为止

3.字符*满足3.1入符号栈，字符5入数栈

4.字符)，满足4.2，将符号栈元素出栈并压入数栈直至(为止

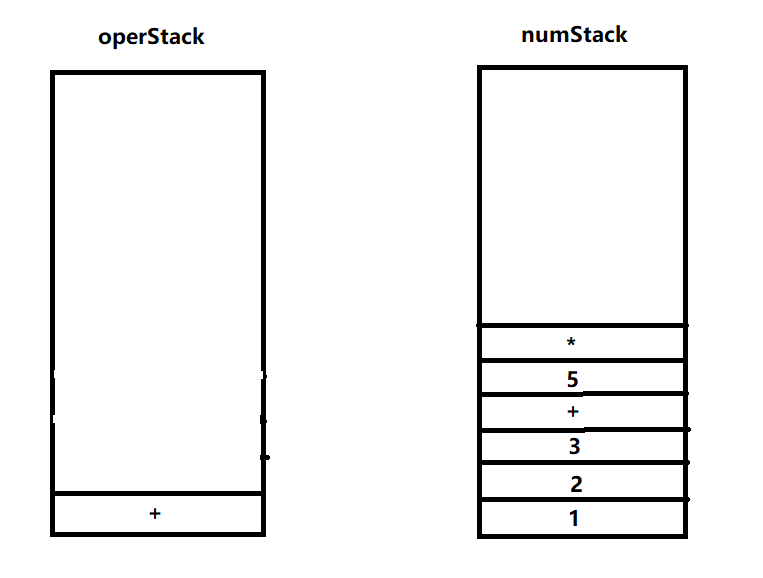
5.字符-，满足3.3，将符号栈栈顶元素出栈，压入数栈，再将字符压入符号栈

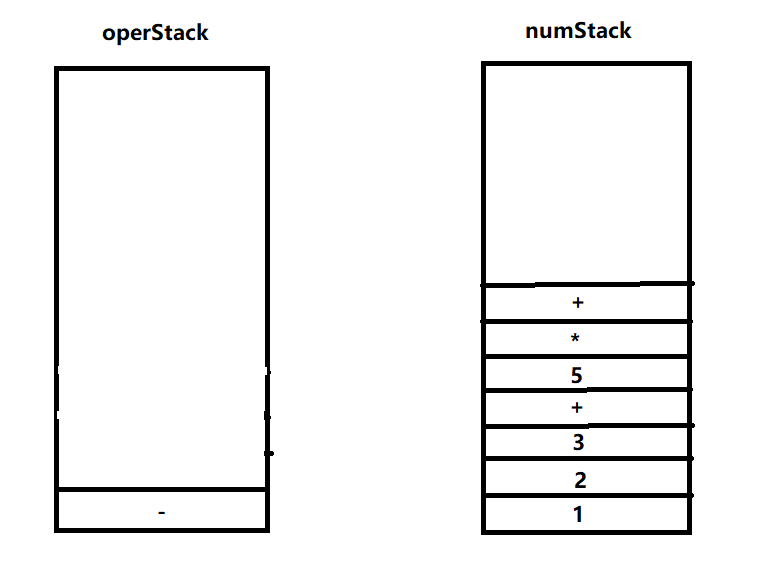
6.6入数栈，/满足3.2入符号栈，2入数栈

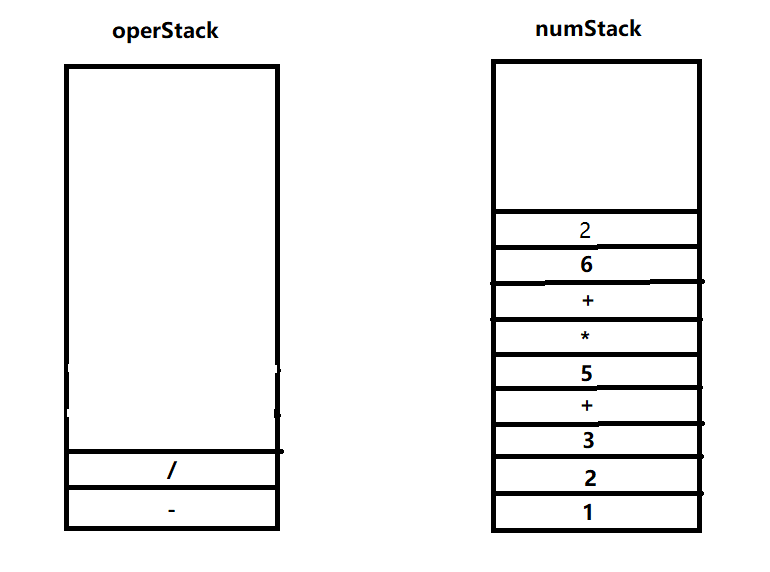
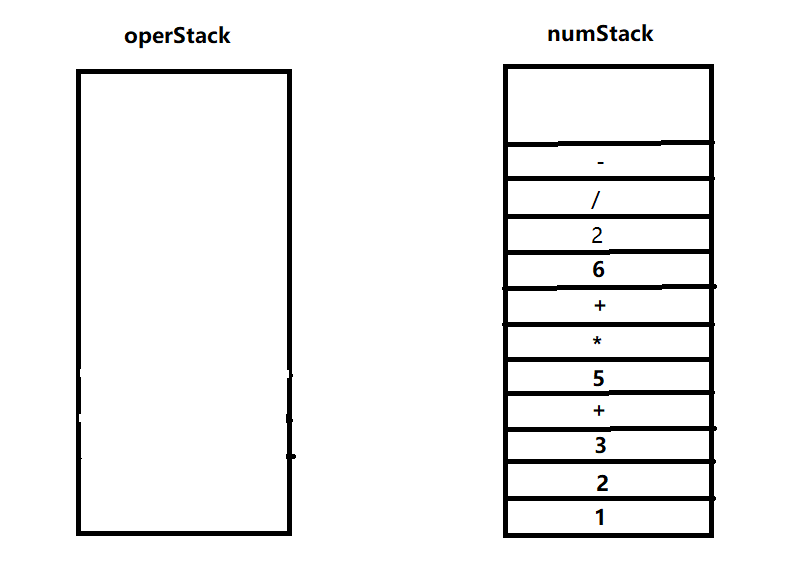
7.循环结束，将符号栈剩余元素压入数栈，之后将数栈元素出栈拼接成字符串，再将字符串逆序，即得到逆波兰表达式1 2 3 + 5 * + 6 2 / -

实现代码

import java.util.Arrays;
import java.util.Stack;

public class InfixToSuffix {
    public String infix;
    public InfixToSuffix(String infix) {
        this.infix = infix;
    }

    public String transform() {
        Stack<String> numStack = new Stack<>();
        Stack<String> operStack = new Stack<>();
        String[] str = infix.split(" ");
        for (int i = 0; i < str.length; i++) {
            String temp = str[i];
            if (temp.matches("\\d+")) {               // 数字
                numStack.push(temp);
            }else if (isOperation(temp)) {         // 操作符
                while (!operStack.isEmpty() && !operStack.peek().equals("(") && priority(temp) <= priority(operStack.peek())){
                    numStack.push(operStack.pop());
                }
                operStack.push(temp);
            }else if (temp.equals("(")){
                operStack.push(temp);
            }else if (temp.equals(")")){
                while (!operStack.peek().equals("(")){
                    numStack.push(operStack.pop());
                }
                operStack.pop();
            }
        }
        // 将剩余操作符入栈
        while (!operStack.isEmpty()){
            numStack.push(operStack.pop());
        }

        // 将数栈元素出栈，得到的是后缀表达式的反序字符串，需要反转一次
        StringBuffer suffix = new StringBuffer();
        while (!numStack.isEmpty()){
            suffix.append(numStack.pop()).append(numStack.isEmpty() ? "" : " ");
        }
        return String.valueOf(suffix.reverse());
    }

    public boolean isOperation(String oper) {
        return oper.equals("+") || oper.equals("-") || oper.equals("*") || oper.equals("/");
    }

    public int priority(String oper) {
        switch (oper) {
            case "+" : case "-" : return 1;
            case "*" : case "/" : return 2;
        }
        return 0;
    }
}

问题

此逆波兰计算器是一个简易版本的计算器，没有异常处理机制、小数运算等，读者可以补充补充，感兴趣的也可以自己写一个逆波兰或者中缀表达式的计算器练练手，才能更好的理解，毕竟提升编程最有效的方法就是敲代码。