陆拾壹的博客

一只超会写bug的程序猿

0%

浅谈KMP

发表于 更新于 分类于 阅读次数：

前言

之前在学数据结构时遇到过模式串匹配问题，当时接触学习过BF算法与KMP算法，只是那时处于一知半解的状态。就在前不久刷题时遇到了有关该算法的题目，就花了不少时间重新学习该算法，学习完也是想写个关于该算法的总结，方便日后查阅。

假设

1
2
3
字符串string，以下简称s；模式串pattern，以下简称p
字符串：BBC ABCDAB ABCDABCDABDE
模式串：ABCDABD

BF算法

算法思想

BF，Brute-Force，也称暴力匹配算法。其思路是将字符串的第一个字符与模式串的第一个字符进行匹配，若相等，则继续比较字符串的第二个字符与模式串的第二个字符；若不等，则比较字符串的第二个字符与模式串的第一个字符。

算法流程

字符串与模式串为上文所做假设，此时假设字符串匹配到i位置，模式串匹配到j位置，则有如下情况：

  1. 当匹配时，即s[i] == p[j]，执行 i++,j++
  2. 当失配时，即s[i] != p[j]，执行 i = i - j + 1,j = 0

1.初始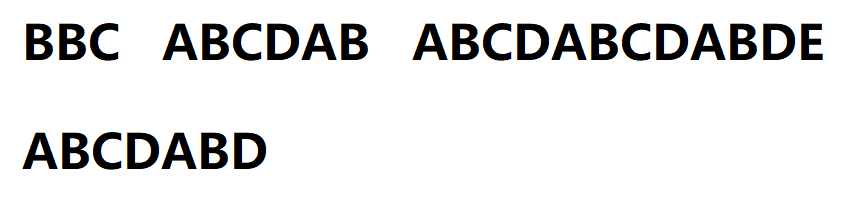
1.1

2.因为s[0] != p[0]，此时失配，执行2：当失配时，即s[i] != p[j]，执行 i = i - j + 1,j = 0，此时判断s[1] == p[0]，直到s[i] = p[j]
2.1
2.2

3.当i = 4，j = 0时，此时s[4] = p[0]，执行1：当匹配时，即s[i] == p[j]，执行 i++,j++，此时判断s[5] == p[1]，直到再次失配或模式串匹配完成返回结果
3.1
3.2

4.当i = 10，j = 6时，此时s[10] != p[6]，即失配，继续执行2，此时i == 5，j = 0，判断s[5] == p[0]，直到再次匹配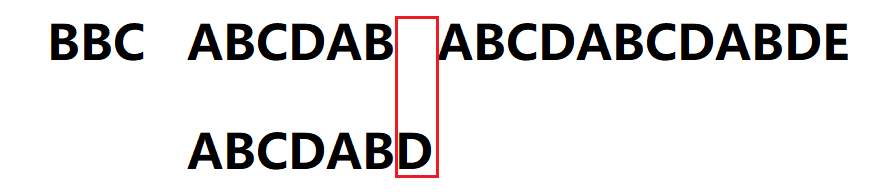
4.1

5.判断s[5] == p[0]，从上步中可以看出，字符串匹配到了s[10]，模式串匹配到了p[6]，但因s[10] != p[6]，所以字符串回溯到了s[5]，而模式串回溯到了p[0]
5.1

总结

通过上面的流程，对BF算法应该有了一定的理解，那么此时不难发现该算法的问题

每次失配时，字符串与模式串都要进行回溯，从3、4、5不难看出该算法做了许多不必要的回溯，第3步的匹配中，我们已经知道s[4] = p[0] = A，s[5] = p[1] = B，所以s[5]与p[0]必失配，而4、5步骤失配后进行回溯，再次比较s[5]与p[0]，显然是无意义的。

这种无意义的匹配大大降低了算法的效率，也不符合我们编程的初衷，所以此时就引入了KMP算法，也是本文的重点算法。

BF实现代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class BF {
    public int BFSearch(String s, String p){
        int n = s.length(), m = p.length();
        int i = 0, j = 0;
        while (i < n && j < m){
            if (s.charAt(i) == p.charAt(j)){
                i++;
                j++;
            }else {
                i = i - j + 1;
                j = 0;
            }
        }
        if (j == m){
            return i - j;
        }
        return -1;
    }
}

KMP算法

算法思想

Knuth-Morris-Pratt，简称KMP算法，由 Donald Knuth、James H. Morris 和 Vaughan Pratt 三人于1977年联合发表的。该算法旨在利用已经匹配的部分字符串的有效信息，来保证i不回溯，只回溯j从而达到将模式串移动到正确匹配位置的目的。

算法流程

先介绍KMP算法流程（若是感到不适看不懂，没关系，先对算法流程大致有个了解），中间细节后面会一一解释，此算法有一定难度，可以反复阅读理解，想掌握就得付出。
字符串与模式串为上文所做假设，此时假设字符串匹配到i位置，模式串匹配到j位置，则有如下情况：

  1. 当j = -1 或 s[i] = p[j]，执行i++，j++
  2. 当j != -1 且 s[i] != p[j]，执行j = next[j]，i不变

看到这，想必许多人都跟我有一样的疑惑：为什么要判断j = -1？next数组是什么？为什么要执行j = next[j]？带着这些疑惑，接着往下走，会慢慢理解的。

步骤

生成next数组

定义

next数组代表当前字符之前的字符串中，有多大长度的前缀后缀。例如，next[j] = k（k是常数），表示j之前的字符串有最大长度为k的前缀后缀。

作用

当失配时，该字符对应的next值会告诉你下一步应该跳到哪个位置（跳到next[j]位置）。当next[j] = 0 或 -1 时，表示跳到开头字符；当next[j] = k 且 k > 0 时，表示模式串跳到j之前的某个字符，并将其接着与字符串进行比较

寻找最长前缀后缀

如果给定的模式串是：“ABCDABD”，从左至右遍历整个模式串，其各个子串的前缀后缀分别如下表格所示：

模式串的各个子串 前缀 后缀 最大公共元素长度
A 空 空 0
AB A B 0
ABC A,AB C,BC 0
ABCD A,AB,ABC D,CD,BCD 0
ABCDA A,AB,ABC,ABCD A,DA,CDA,BCDA 1
ABCDAB A,AB,ABC,ABCD,ABCDA B,AB,DAB,CDAB,BCDAB 2
ABCDABD A,AB,ABC,ABCD,ABCDA,ABCDAB D,BD,ABD,DABD,CDABD,BCDABD 0

也就是说，原模式串子串对应的各个前缀后缀的公共元素的最大长度表为（下简称《最大长度表》）：

模式串 A B C D A B D
前后缀最大公共元素长度 0 0 0 0 1 2 0

基于最大长度表匹配

模式串移动位数 = 已匹配字符数 - 失配字符的上一位字符所对应的最大长度值

1.初始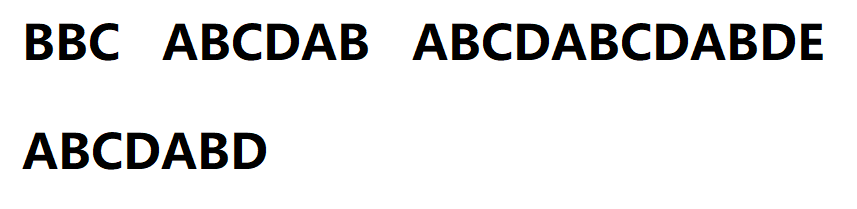
1.1

2.前面失配，直到字符串的第5个字符A时开始匹配
2.1
2.2

3.从A匹配时，直到i = 10，j = 6再次失配，此时模式串需要向右移动，模式串移动位数 = 已匹配字符数 - 失配字符的上一位字符所对应的最大长度值，即移动6 - 2 = 4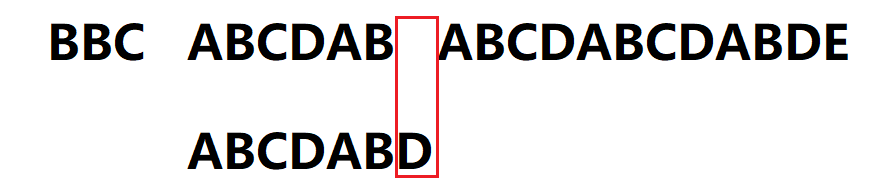
3.1
3.2

4.C与空格再次失配，模式串移动：已匹配字符数2 - 前一字符B对应的最大长度表的值0 = 2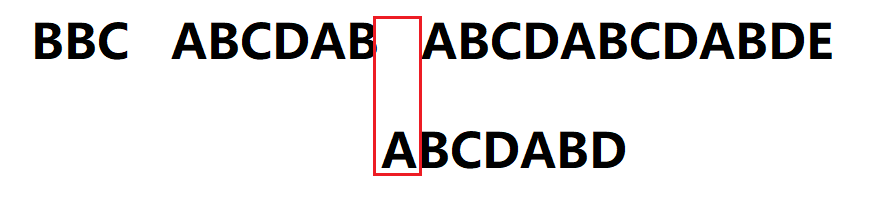
4.1

5.A与空格失配，此时模式串已定位到开头字符仍与此时的字符失配，说明此时的字符及之前的字符串未能正确匹配模式串，模式串向右移动一位，舍弃前面的字符串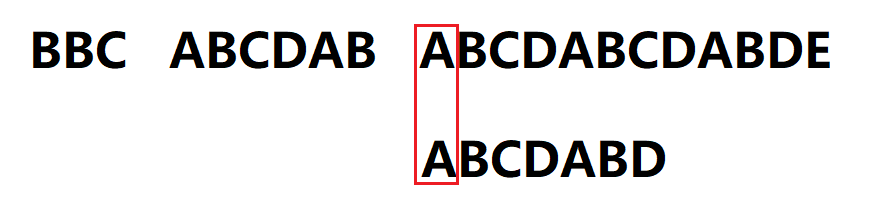
5.1

6.直到D与C再次失配，此时模式串移动：已匹配字符数6 - 前一字符B对应的最大长度表的值2 = 4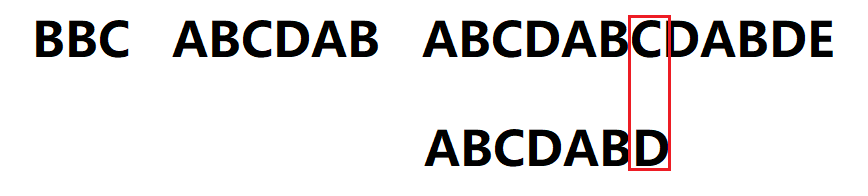
6.1
6.2

7.匹配成功

根据最大长度表求next数组

next的出现

由上文，我们已经知道，字符串“ABCDABD”各个前缀后缀的最大公共元素长度分别为：

模式串 A B C D A B D
最大前后缀公共元素长度 0 0 0 0 1 2 0

并且由此表得出如下结论：

失配时，模式串移动位数 = 已匹配字符数 - 失配字符的上一位字符所对应最大长度值

通过如上结论以及实际匹配，我们发现模式串移动位数与当前失配字符无关，失配时都是看上一字符对应的最大长度值，由此引出了next数组

字符串ABCDABD的next数组如下：

模式串 A B C D A B D
next -1 0 0 0 0 1 2

将最大长度表与next数组合并，如下图所示：

模式串 A B C D A B D
前后缀最大公共元素长度 0 0 0 0 1 2 0
next -1 0 0 0 0 1 2

观察合并后的表，可以看出next数组与最大长度表的关系

最大长度表右移一位，初值赋为-1，即得到了next数组
最大长度表：模式串移动位数 = 已匹配字符数 - 失配字符的上一位字符所对应的最大长度值
next数组 ：模式串移动位数 = 失配字符位置 - 失配字符对应的next的值
值得注意的是，因为数组从0开始计数，所以已匹配字符数 = 失配字符位置，失配字符的上一位字符所对应的最大长度值 = 失配字符对应的next的值，所以最大长度表的模式串移动位数 = next数组的模式串移动位数

总结：next数组就是求模式串的最大前缀后缀长度，然后右移一位，初值赋为-1

计算next

1.如果对于值k，已有p0,p1,…,pk-1 = pj-k,pj-k+1,…,pj-1，相当于next[j] = k

  • 可以理解为j之前的字符串有最大长度为k的前后缀，当在j失配时，j = next[j] = k，此时的next[j]正是j之前的字符串的最大前后缀长度，相当于模式串向右移动了j - next[j]，即下一步匹配s[i]与p[k]。举个例子，如下图所示，当i = 10，j = 6失配，执行i不变，j = next[j] = 2，相当于模式串移动失配字符位置6 - 失配字符所对应的next值2 = 4
    3.1
    3.2

2.此时还有个问题，就是已知next[0,…,j]，如何求next[j + 1]？

  • 关于该问题的提出，我是这样理解的，next[j]初始是next[0] = -1，next[1] = 0，next[2]…next[j]需要求，通过上述推导求出next[2]，相当于next[1]求出next[2]，依靠这两个推导就能求出字符串的next数组，也就是递推求解next数组

求next[j + 1]时会遇到如下两种情况：

  • 当p[k] = p[j]，next[j + 1] = next[j] + 1 = k + 1；
    • 可以这样理解，p0,p1,...,pk-1 = pj-k,pj-k+1,...,pj-1，相当于next[j] = k，而p[k] = p[j]相当于p0,p1,...pk-1,pk = pj-k,pj-k+1,...pj-1,pj，也就是next[j + 1] = next[j] + 1 = k + 1
  • 当p[k] != p[j]，k = next[k]回溯，如果p[next[k]] = p[j]，那么next[j + 1] = next[k] + 1；如果p[next[k]] != p[j]，那么k继续回溯，直至0或-1

假设模式串ABACABABC，接下来将举例来理解这两种情况
当p[k] = p[j]，如下图所示，k = 2，j = 6，此时p[k] = p [j] = A，相当于p0,p1...pk-1,pk = pj-k,pj-k+1,...pj-1,pj，所以next[j + 1] = next[j] + 1 = k + 1

模式串 A B A C A B A B C
前后缀相同长度 0 0 1 0 1 2 3 2 0
next值 -1 0 0 1 0 1 2 3 2
索引 p0 pk-1 pk pk+1 pj-k pj-1 pj pj+1 pj+2

当p[k] != p[j]，如下图所示，k = 3，j = 7，此时p[k] != [j]，执行k = next[k] = 1回溯，p[next[k]] = p[j]，所以此时next[j + 1] = next[k] + 1

模式串 A B A C A B A B C
前后缀相同长度 0 0 1 0 1 2 3 2 0
next值 -1 0 0 1 0 1 2 3 2
索引 p0 pk-2 pk-1 pk pj-k pj-1 pj-2 pj pj+1

总结
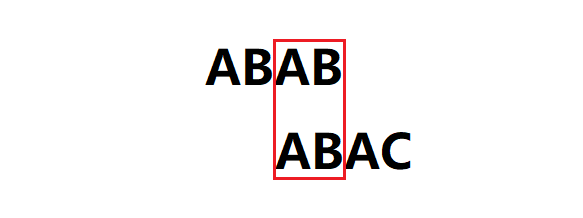
关于上述例子p[k] != p[j]，我觉得可以这样理解，将其想象成字符串ABAB与模式串ABAC进行匹配，如下图所示，此时C与B失配，通过next数组对模式串ABAC右移，右移位数 = 失配字符位置3 - 失配字符对应的next值1 = 2，此时字符串ABAB的第二个AB与模式串AB匹配，所以next[j + 1] = 2。说到这里，就不得不提以下几点：

  1. 为什么是字符串ABAB与模式串ABAC，而不是字符串ABAC与模式串ABAB呢？
  • 因为ABAC的next值已计算好，在字符串与模式串进行匹配时，就是在利用模式串的next值对模式串进行回溯，所以将有next值的ABAC想象成模式串
  1. 这样想象有什么好处？
  • 回想下KMP算法字符串与模式串的匹配过程，就会发现字符串与模式串的匹配与模式串计算next值的过程其实是一样的，这样也有利于理解代码中的k = next[k]，这句代码用来实现k回溯，不仅是在编程计算next数组，还是在匹配模式串时都有这句代码，当时学习时在计算next数组的代码中一直不理解这句代码的含义，后来这样想象相对好理解些。
    1.1
    1.2

基于next数组进行匹配

模式串ABCDABD的next数组如下：

模式串 A B C D A B D
next -1 0 0 0 0 1 2

1.初始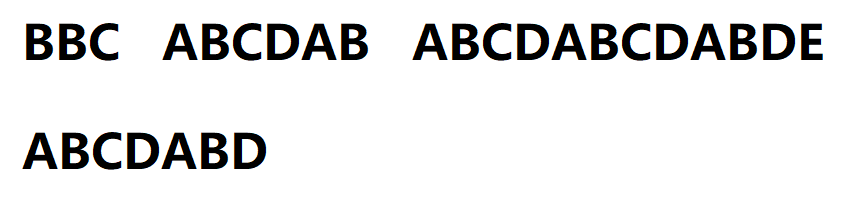
1.1

2.因为i = 0，j = 0，s[i] != p[j]，失配，执行2：当j != -1 且 s[i] != p[j]，执行j = next[j]，i不变，此时j = -1，i = 0
2.1

3.因为j = -1，执行1：当j = -1 或 s[i] = p[j]，执行i++，j++，此时i = 1，j = 0，s[1] != p[0]，再次失配，j = next[j] = -1，再次变为-1，再次执行1，重复上述过程，直至s[i] = p[j]
3.1

4.当i = 4，j = 0，此时s[i] = p[j]，执行1，直到失配或者匹配完成
4.1

5.当i = 10，j = 6失配，执行2，j = next[j] = 2，模式串右移位数 = 失配字符位置6 - 失配字符对应的next值2 = 4，继续判断s[10] == p[2]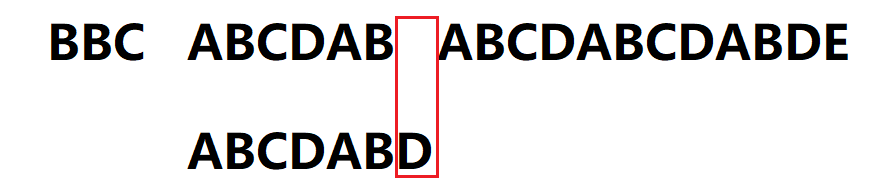
5.1
5.2

6.s[10] != p[2]，j = next[j] = 0，继续判断s[10] == p[0]，仍然失配，继续回溯j = next[j] = -1。因为j = -1，执行1，i = 11，j = 0，继续判断s[11] == p[0]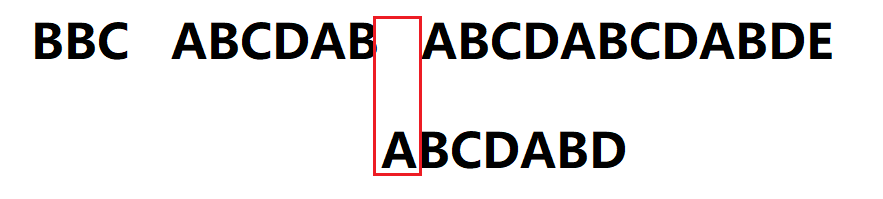
6.1
6.2

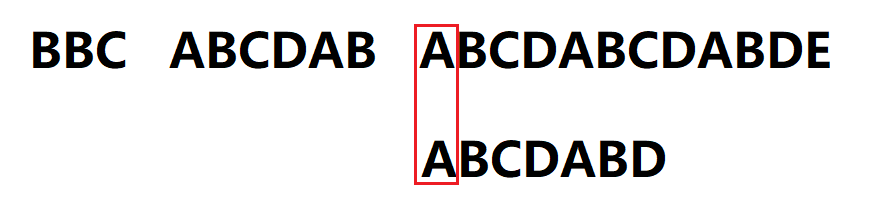
7.直到D与C再次失配，执行j = next[j] = 2，模式串移动位数 = 失配字符位置6 - 失配字符对应的next值2 = 4，再次匹配，最后匹配成功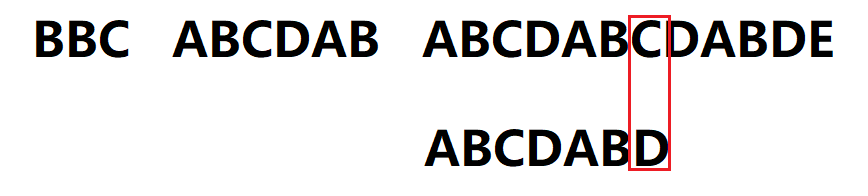
7.1
7.2

基于next数组的匹配过程与基于最大长度表的匹配过程是一样的，也证明了next数组与最大长度表的关系

总结

1.为什么要判断j = -1？

从上面的3和6不难看出，j变为-1时，必先变为0，代表在匹配过程中，因为失配j不断回溯，直到回到开头字符，也就是j = 0，此时如果开头字符也失配，说明当前字符串失配字符位置往前的字符串不能匹配模式串了，舍弃前面已判断的字符串，从失配字符的下一个字符开始与模式串的开头字符继续匹配，也可以理解为重头再来，对比初始图与6的第二张图会比较好理解。

2.next数组是什么？

next数组是计算最大前后缀长度值并右移一位，初值赋为-1的数组

3.为什么要执行j = next[j]？

简单说就是模式串回溯，在计算next中最后的总结已有解答，参考实例也会更容易理解些

KMP实现代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class KMP {
    public int KmpSearch(String s, String p){
        if ("".equals(p)){
            return -1;
        }
        int[] next = getNext(s);
        int i = 0, j = 0;
        while (i < s.length() && j < p.length()){
            if (j == -1 || s.charAt(i) == p.charAt(j)){
                i++;
                j++;
            }else {
                j = next[j];        // 算法核心
            }
        }
        if (j == p.length()){
            return i - j;
        }
        return -1;
    }
    public int[] getNext(String p){
        int[] next = new int[p.length()];
        next[0] = -1;
        int i = 0, j = -1;
        while (i < p.length() - 1){
            if (j == -1 || p.charAt(i) == p.charAt(j)){
                next[++i] = ++j;
            }else {
                j = next[j];        // 算法核心
            }
        }
        return next;
    }
}

参考文章

参考文章1