陆拾壹的博客

一只超会写bug的程序猿

0%

力扣每日一题2021/7/22

发表于 更新于 分类于 ， 阅读次数：

题目：旋转图像

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

难度：中等

示例 1：

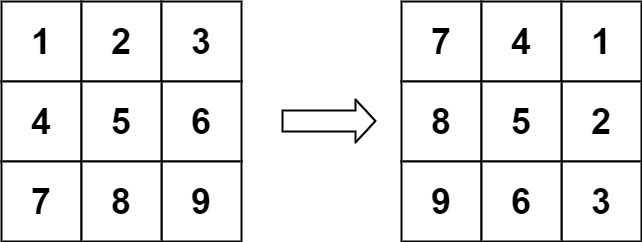
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

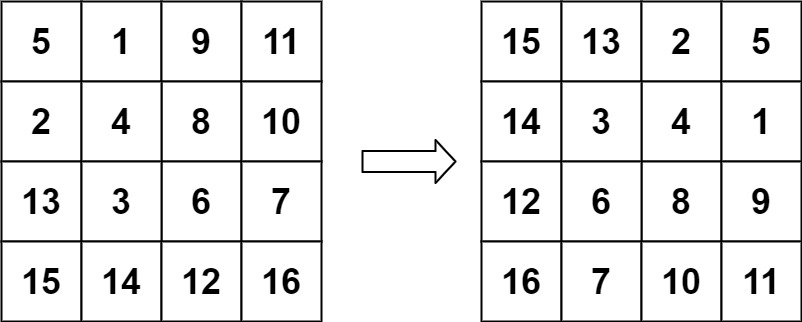
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

示例 3：

输入：matrix = [[1]]
输出：[[1]]

示例 4：

输入：matrix = [[1,2],[3,4]]
输出：[[3,1],[4,2]]

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/rotate-image
著作权归领扣网络所有。商业转载请联系官方获得授权，非商业转载请注明出处。

解题思路

  1. 使用辅助数组
  2. 原地旋转
  3. 用翻转代替旋转

解题代码

原地旋转

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public void rotate(int[][] matrix) {
        int rotation = (int)(Math.ceil(matrix.length / 2.0));
        int length = matrix.length;
        for (int i = 0; i < matrix.length - rotation; i++){
            for (int j = 0; j < rotation; j++){
                int temp = matrix[i][j];
                matrix[i][j] = matrix[length - j - 1][i];
                matrix[length - j - 1][i] = matrix[length - i - 1][length - j - 1];
                matrix[length - i - 1][length - j - 1] = matrix[j][length - i - 1];
                matrix[j][length - i - 1] = temp;
            }
        }
    }
}

官方解题代码

使用辅助数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        int[][] matrix_new = new int[n][n];
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                matrix_new[j][n - i - 1] = matrix[i][j];
            }
        }
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                matrix[i][j] = matrix_new[i][j];
            }
        }
    }
}

原地旋转

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        for (int i = 0; i < n / 2; ++i) {
            for (int j = 0; j < (n + 1) / 2; ++j) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n - j - 1][i];
                matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
                matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
                matrix[j][n - i - 1] = temp;
            }
        }
    }
}

用翻转代替旋转

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        // 水平翻转
        for (int i = 0; i < n / 2; ++i) {
            for (int j = 0; j < n; ++j) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n - i - 1][j];
                matrix[n - i - 1][j] = temp;
            }
        }
        // 主对角线翻转
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < i; ++j) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }
        }
    }
}