前言
在学习数据结构与算法时,一定会接触到几大经典排序算法,因为排序算法有点多,学习完时想将其做一个总结,以便之后有所遗忘时能快速阅读复习。
概述
排序算法,将一组或多组数据按照一个或多个关键字的大小进行重新排序的算法。
分类
排序算法根据数据大小不同使得排序过程使用的存储器不同可分为:内部排序(内存)、外部排序(内外存结合),我们主要学习内部排序,内部排序又可细分如下:
1.插入排序
- 直接插入排序
- 希尔排序
2.选择排序
- 简单选择排序
- 堆排序
3.交换排序
- 冒泡排序
- 快速排序
4.归并排序
5.基数排序
假设数据
1
2
| 排序前:18, 3, 478, 54, 555, 75
排序后:3, 18, 54, 75, 478, 555
|
算法分析
冒泡排序
原理
两两比较,将较大的元素交换到后面,就像气泡浮出水面一样(升序)
思路
1.取出当前元素与下一元素进行比较,当前元素大于下一元素时与下一元素进行交换
2.重复步骤1,直到扫描完未排序序列(一趟排序即确定一个较大元素已在序列末尾排好序)
3.重复步骤1、2,完成排序
算法图解

代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| import java.util.Arrays;
public class BubbleSort {
public static void bubbleSort(int[] nums) {
for (int i = 1; i < nums.length; i++) {
for (int j = 0; j < nums.length - i; j++) {
if (nums[j] > nums[j + 1]) {
int temp = nums[j];
nums[j] = nums[j + 1];
nums[j + 1] = temp;
}
}
}
}
public static void bubbleSort2(int[] nums) {
for (int i = 1; i < nums.length; i++) {
boolean flag = false;
for (int j = 0; j < nums.length - i; j++) {
if (nums[j] > nums[j + 1]) {
int temp = nums[j];
nums[j] = nums[j + 1];
nums[j + 1] = temp;
flag = true;
}
}
if (!flag) {
break;
}
}
}
public static void main(String[] args) {
int[] nums = {18,3,478,54,555,75};
bubbleSort(nums);
System.out.println(Arrays.toString(nums));
}
}
|
简单选择排序
原理
取出一个元素,将该元素与其之后的元素进行比较,找出一个最小值跟该元素进行交换(升序)
思路
1.取出一个元素min,遍历该元素之后的所有元素,若min > 该元素(未排序元素),min = 该元素
2.重复步骤1,完成排序
算法图解
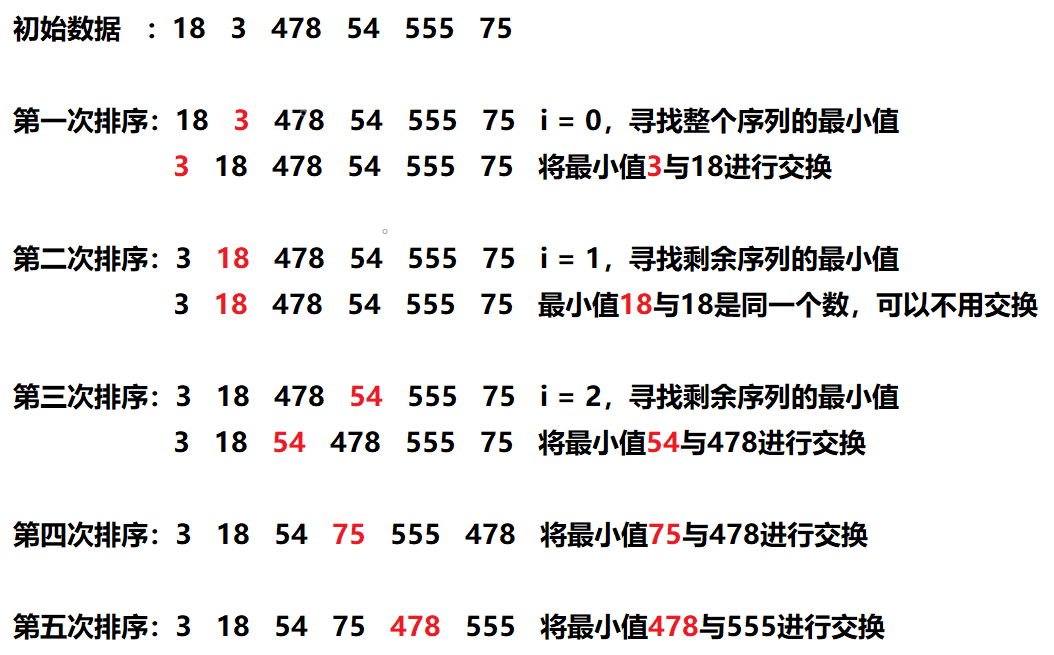
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| import java.util.Arrays;
public class SelectSort {
public static void selectSort(int[] nums) {
for (int i = 0; i < nums.length - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < nums.length; j++) {
if (nums[minIndex] > nums[j]) {
minIndex = j;
}
}
if (minIndex != i) {
int temp = nums[i];
nums[i] = nums[minIndex];
nums[minIndex] = temp;
}
}
}
public static void main(String[] args) {
int[] nums = {18, 3, 478, 54, 555, 75};
selectSort(nums);
System.out.println(Arrays.toString(nums));
}
}
|
直接插入排序
原理
构建一个有序序列,从后向前遍历有序序列寻找相应位置,将无序数据一一插入。
思路
1.默认第一个元素已排序,即有序序列
2.取出下一元素,设为待插入元素,从后向前遍历有序序列,若该元素(已排序序列)大于待插入元素,则将该元素后移
3.重复步骤2,直到找到该元素小于或等于待插入元素的位置,插入元素
4.重复步骤2、3,完成排序
算法图解

代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| import java.util.Arrays;
public class InsertSort {
public static void insertSort(int[] nums) {
for (int i = 1; i < nums.length; i++) {
int insertIndex = i;
int insertVal = nums[insertIndex];
for (int j = i - 1; j >= 0; j--) {
if (insertVal > nums[j]) {
break;
}
nums[insertIndex--] = nums[j];
}
nums[insertIndex] = insertVal;
}
}
public static void main(String[] args) {
int[] nums = {18,3,478,54,555,75};
insertSort(nums);
System.out.println(Arrays.toString(nums));
}
}
|
希尔排序
原理
将待排序序列进行分组,对每个分组采用插入排序,不断缩小分组直至分组为1
思路
1.设序列长度为n,分组依次为n/2、n/4
2.默认每组第一个元素为有序序列,对于同一组,取出下一元素设为待插入元素,若该元素大于待插入元素,则将该元素后移
3.重复步骤2,直至找到元素小于等于待插入元素的位置,插入元素
4.重复步骤2、3,完成排序
算法图解
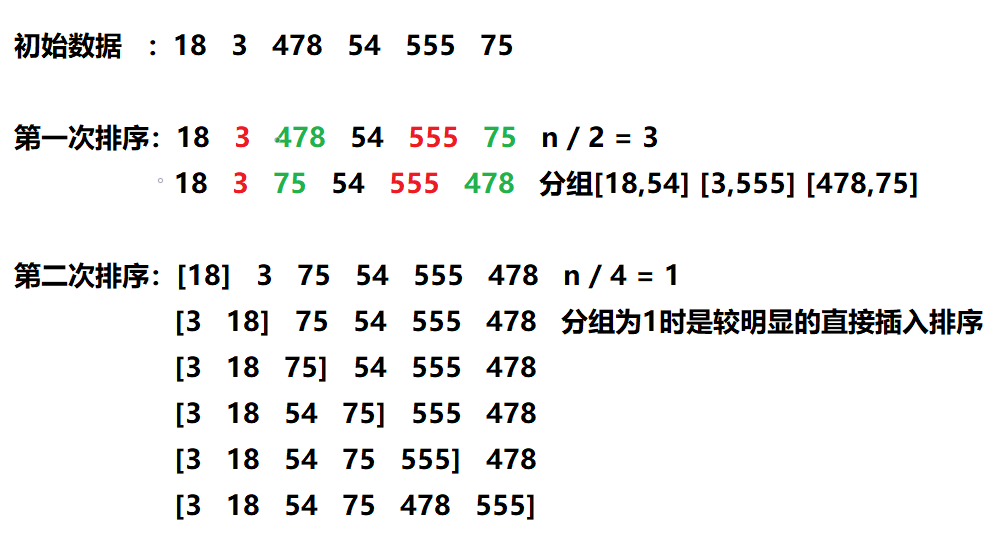
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| import java.util.Arrays;
public class ShellSort {
public static void shellSort(int[] nums) {
for (int gap = nums.length / 2; gap > 0; gap /= 2) {
for (int i = gap; i < nums.length; i++) {
int insertIndex = i;
int insertVal = nums[i];
while (insertIndex - gap >= 0 && insertVal < nums[insertIndex - gap]) {
nums[insertIndex] = nums[insertIndex - gap];
insertIndex -= gap;
}
nums[insertIndex] = insertVal;
}
}
}
public static void main(String[] args) {
int[] nums = {18,3,478,54,555,75};
shellSort(nums);
System.out.println(Arrays.toString(nums));
}
}
|
快速排序
原理
取第一个数作为基准值,分别在左边寻找比基准值大的数,在右边寻找比基准值小的数进行交换。
思路
1.选取一个数作为基准值
2.重新排序,比基准值小的元素放在基准值前面,比基准值大的元素放在基准值后面,最后基准值将处于序列中间位置(中间位置指:基准值左边元素都小于基准值,右边元素都大于基准值)
3.递归地对小于基准值的子序列和大于基准值的子序列进行重新排序
算法图解
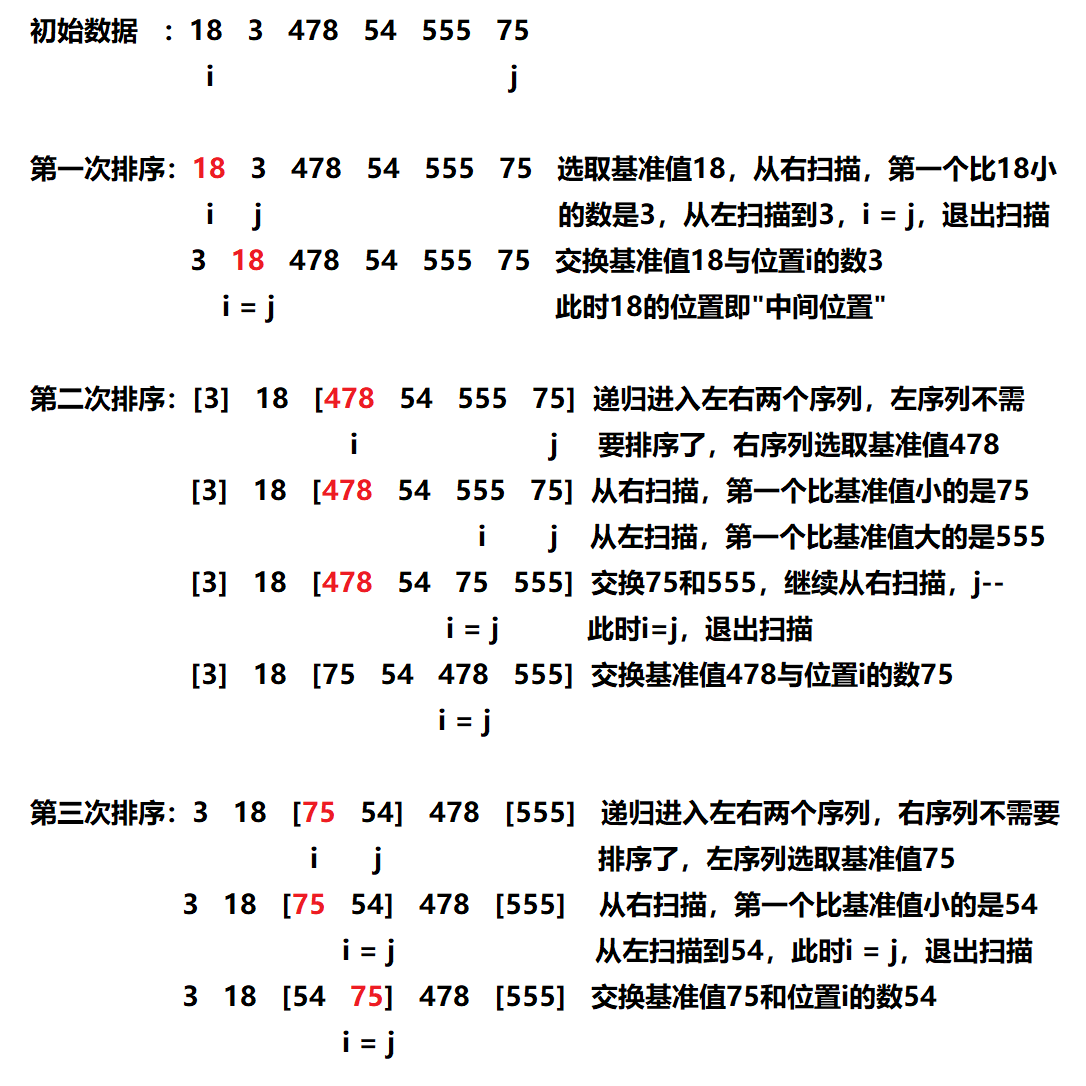
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| import java.util.Arrays;
public class QuickSort {
public static void quickSort(int[] nums) {
quickSort(nums, 0, nums.length - 1);
}
public static void quickSort(int[] nums, int left, int right) {
if (left > right) {
return;
}
int temp = nums[left];
int i = left, j = right;
while (i < j) {
while (i < j && temp <= nums[j]) {
j--;
}
while (i < j && temp >= nums[i]) {
i++;
}
if (i < j) {
int t = nums[i];
nums[i] = nums[j];
nums[j] = t;
}
}
nums[left] = nums[i];
nums[i] = temp;
quickSort(nums, left, i - 1);
quickSort(nums, i + 1, right);
}
public static void main(String[] args) {
int[] nums = {18,3,478,54,555,75};
quickSort(nums);
System.out.println(Arrays.toString(nums));
}
}
|
归并排序
原理
将待排序的元素分成两个大小大致相同的子集合,分别对两个子集合排序,最终将子集合合并为排好序的集合
思路
1.取中间元素,对左右两边进行递归排序
2.声明两个指针指向左右两个子集合的初始位置
3.声明一个临时空间,比较指针指向的元素大小,小的先放入临时空间,存放完再将临时空间的元素放入原数组
算法图解
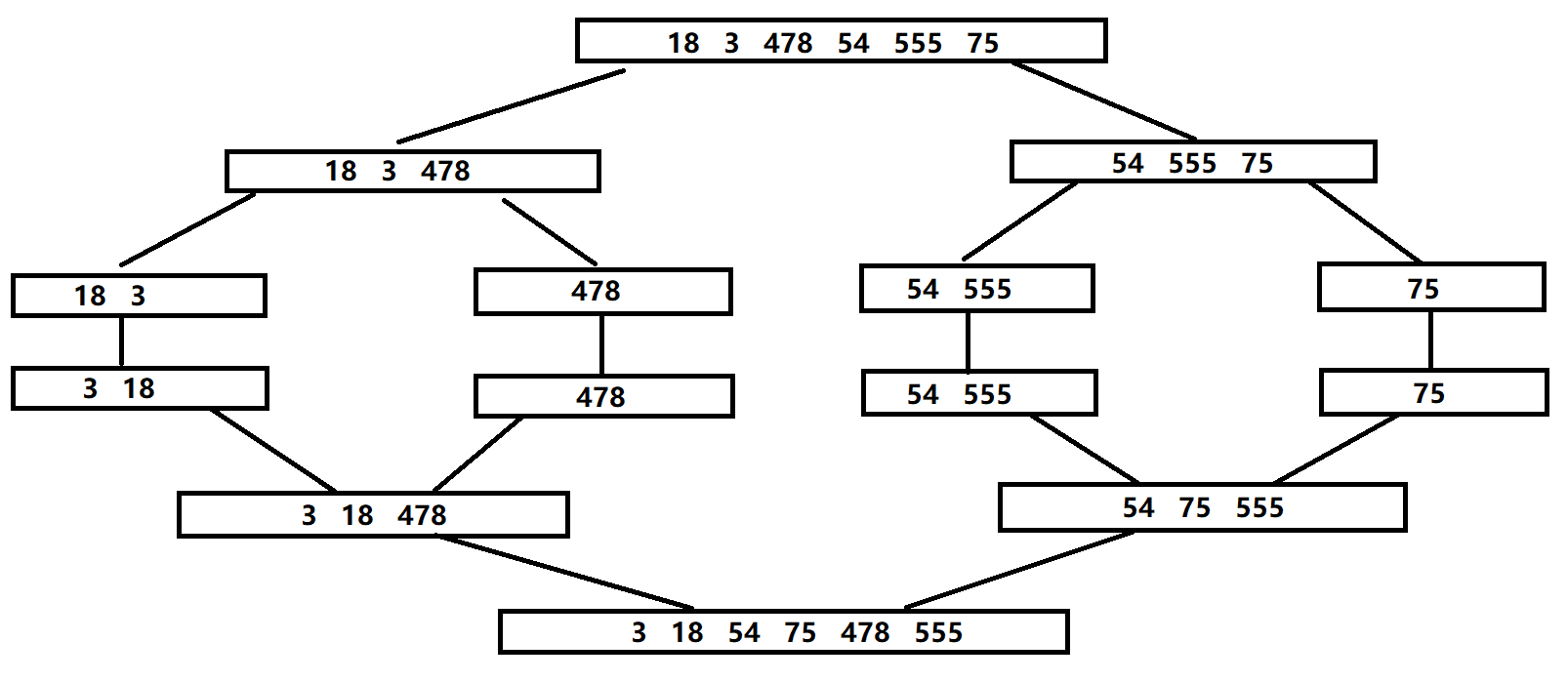
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| import java.util.Arrays;
public class mergeSort {
public static void mergeSort(int[] nums) {
mergeSort(nums, 0, nums.length - 1, new int[nums.length]);
}
public static void mergeSort(int[] nums, int left, int right, int[] temp) {
if (left < right) {
int mid = (left + right) / 2;
mergeSort(nums, left, mid, temp);
mergeSort(nums, mid + 1, right, temp);
merge(nums, left, mid, right, temp);
}
}
public static void merge(int[] nums, int left, int mid, int right, int[] temp) {
int i = left, j = mid + 1, index = 0;
while (i <= mid && j <= right) {
if (nums[i] <= nums[j]) {
temp[index++] = nums[i++];
} else {
temp[index++] = nums[j++];
}
}
while (i <= mid) {
temp[index++] = nums[i++];
}
while (j <= right) {
temp[index++] = nums[j++];
}
for (int k = 0; k < index; k++) {
nums[left + k] = temp[k];
}
}
public static void main(String[] args) {
int[] nums = {18,3,478,54,555,75};
mergeSort(nums);
System.out.println(Arrays.toString(nums));
}
}
|
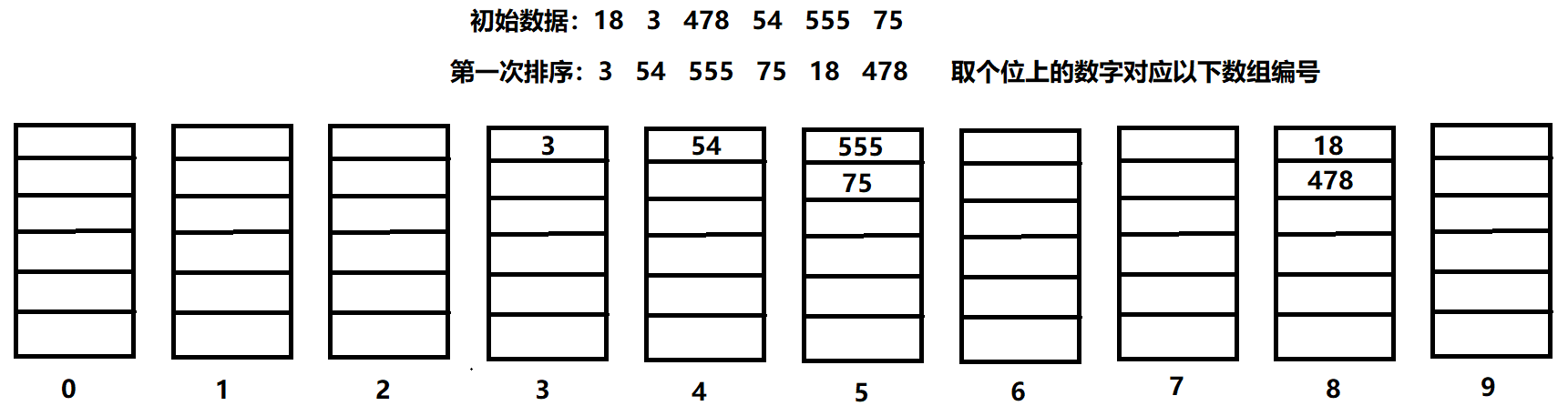
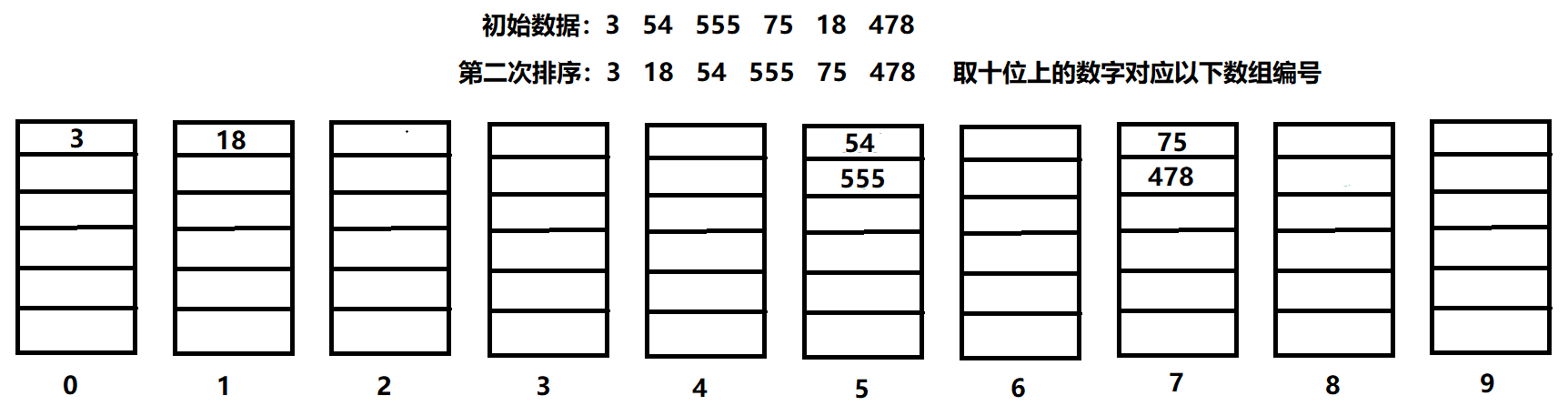
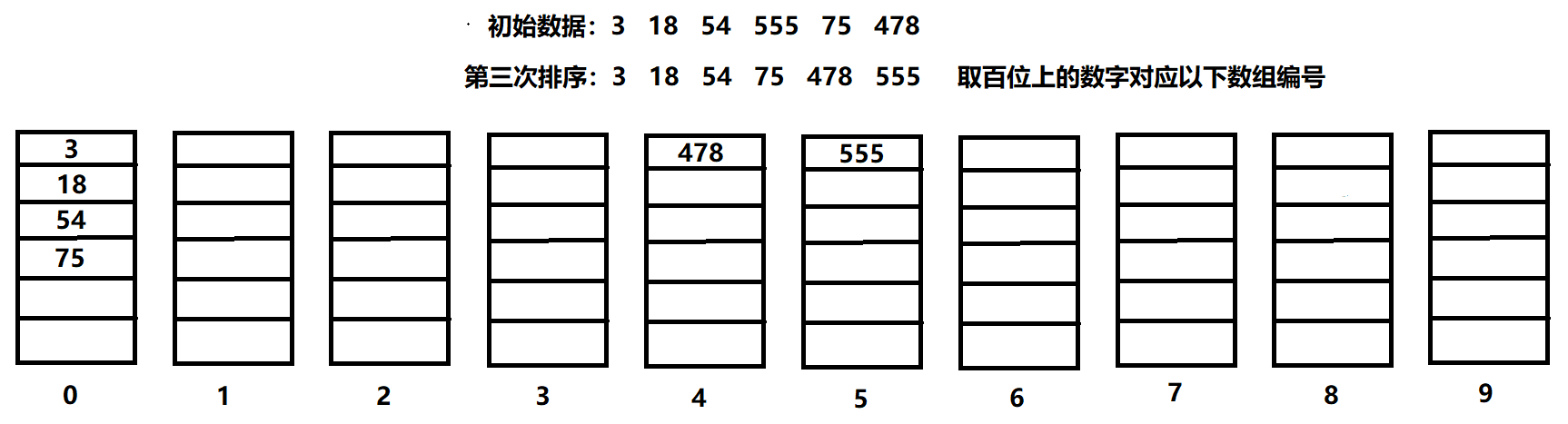
基数排序
原理
将待排序元素统一为数位相同的元素进行比较,数位短的前面补0,从低位开始一一排序直到最高位结束,完成排序
思路
1.声明二维数组buckets作为桶(长10列为元素个数),声明一维数组count记录桶中元素个数
2.扫描元素,将元素放入其个位(之后取十、百、千位)上的数字对应的桶中,并用数组count记录各个桶的元素个数
3.扫描buckets,通过count取出各个桶中的元素,覆盖原序列
4.重复步骤2、3,完成排序
算法图解
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| import java.util.Arrays;
public class radixSort {
public static void radixSort(int[] nums) {
int max = Integer.MIN_VALUE;
for (int i : nums) {
max = Math.max(max, i);
}
int[][] buckets = new int[10][nums.length];
int[] count = new int[10];
for (int exp = 1; max / exp > 0; exp *= 10) {
for (int i = 0; i < nums.length; i++) {
int position = (nums[i] / exp) % 10;
buckets[position][count[position]++] = nums[i];
}
int index = 0;
for (int i = 0; i < count.length; i++) {
if (count[i] > 0) {
for (int j = 0; j < count[i]; j++) {
nums[index++] = buckets[i][j];
}
count[i] = 0;
}
}
}
}
public static void main(String[] args) {
int[] nums = {18,3,478,54,555,75};
radixSort(nums);
System.out.println(Arrays.toString(nums));
}
}
|








